274. H-Index
Given an array of integers citations where citations[i] is the number of citations a researcher received for their ith paper, return the researcher's h-index.
According to the definition of h-index on Wikipedia: The h-index is defined as the maximum value of h such that the given researcher has published at least h papers that have each been cited at least h times.
Example 1:
Input: citations = [3,0,6,1,5]
Output: 3
Explanation: [3,0,6,1,5] means the researcher has 5 papers in total and each of them had received 3, 0, 6, 1, 5 citations respectively.
Since the researcher has 3 papers with at least 3 citations each and the remaining two with no more than 3 citations each, their h-index is 3.
Example 2:
Constraints:
n == citations.length1 <= n <= 50000 <= citations[i] <= 1000
Solution:
首先解释下示例 1 是怎么算的:
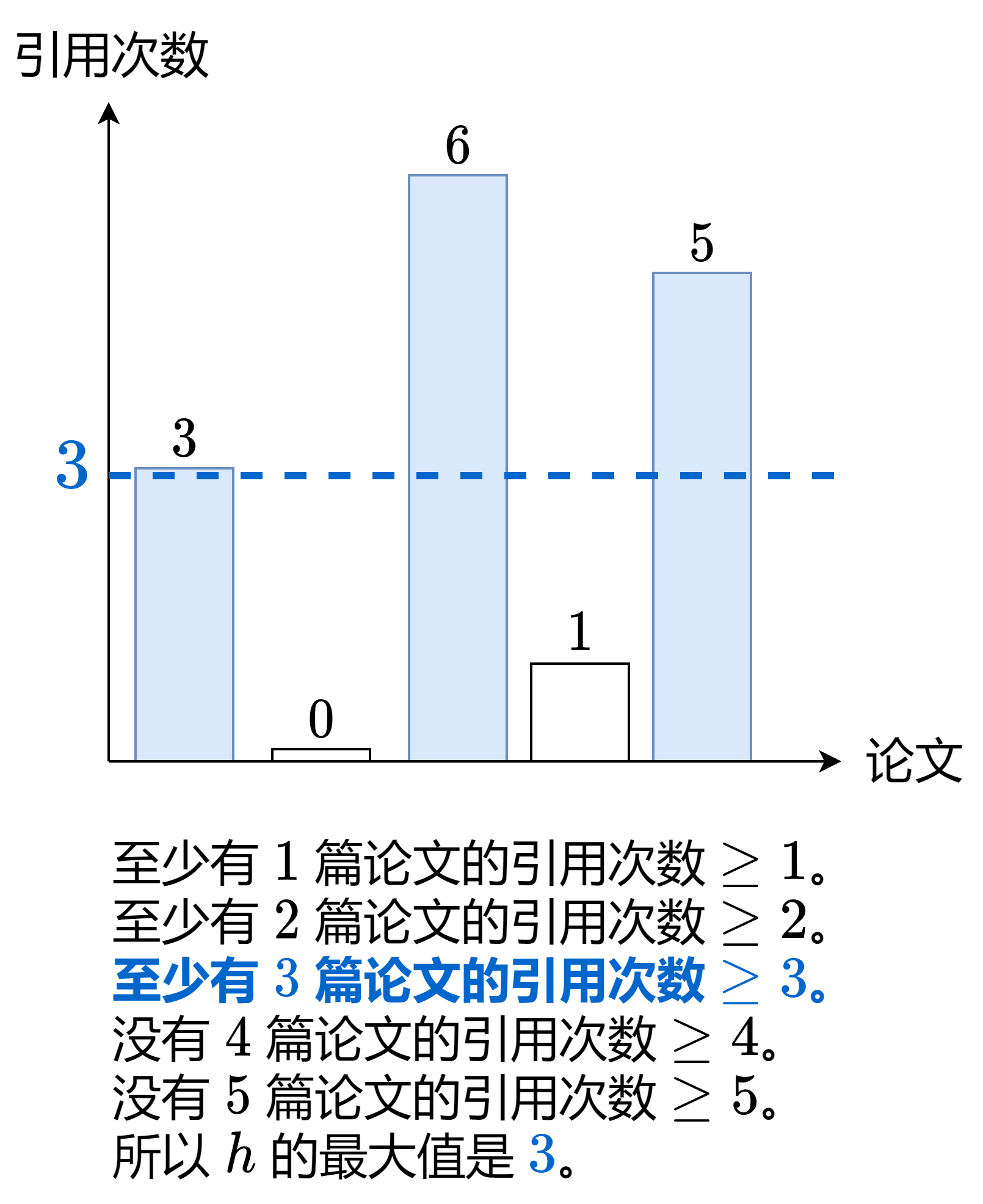
题意:给你一个数组,求一个最大的 h,使得数组中有至少 h 个数都大于等于 h。
本题可以做到 O(n) 时间。
设 n 为 citations 的长度,即这名研究者发表的论文数。根据题意,h 不可能超过 n,所以对于引用次数大于 n 的论文,我们在统计的时候,可以看成是引用次数等于 n 的论文。例如 n=5,假设 h 是 5,那么无论引用次数是 6 还是 5,都满足 ≥5,所以 6 可以看成是 5,毕竟我们只需要统计有多少个数字是 ≥5 的。
所以,创建一个长为 n+1 的 cnt 数组,统计 min(citations[i],n) 的出现次数。
设 s 为引用次数 ≥i 的论文数,我们需要算出满足 s≥i 的最大的 i。
为了快速算出有多少论文的引用次数 ≥i,我们可以从 i=n 开始倒序循环,每次循环,把 cnt[i] 加到 s 中。由于我们是倒序循环的,只要 s≥i 成立,此时的 i 就是满足 s≥i 的最大的 i,直接返回 i 作为答案。
例如示例 1,从 i=5 开始:
i=5,现在 s=2<i,继续循环。 i=4,现在 s=2<i,继续循环。 i=3,现在 s=3≥i,返回 3。
class Solution {
public int hIndex(int[] citations) {
int n = citations.length;
int[] cnt = new int[n + 1];
for (int c : citations){
cnt[Math.min(c, n)]++; // 引用次数 > n, 等价于引用次数为n
}
int s = 0;
for (int i = n; ; i--){ // i = 0的时候, s >= i 一定成j立
s = s + cnt[ij j;
if (s >= i){ // 说明至少i篇论文的引用次数至少为i
return i;
}
}
}
}
// 时间复杂度:O(n),其中 n 为 citations 的长度。
// 空间复杂度:O(n)。