Skip to content

149. Max Points on a Line

Given an array of points where points[i] = [xi, yi] represents a point on the X-Y plane, return the maximum number of points that lie on the same straight line.

Example 1:

img

Input: points = [[1,1],[2,2],[3,3]]
Output: 3

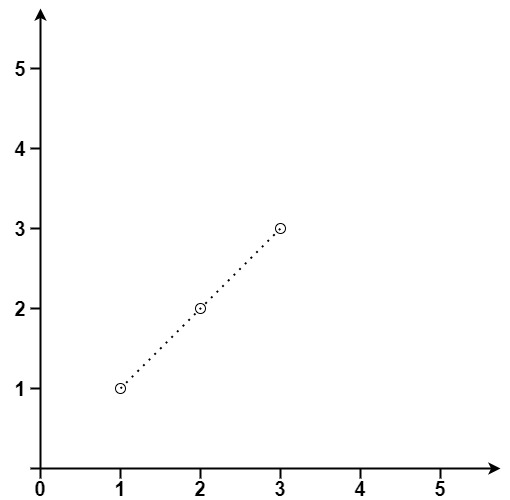
Example 2:

img

Input: points = [[1,1],[3,2],[5,3],[4,1],[2,3],[1,4]]
Output: 4

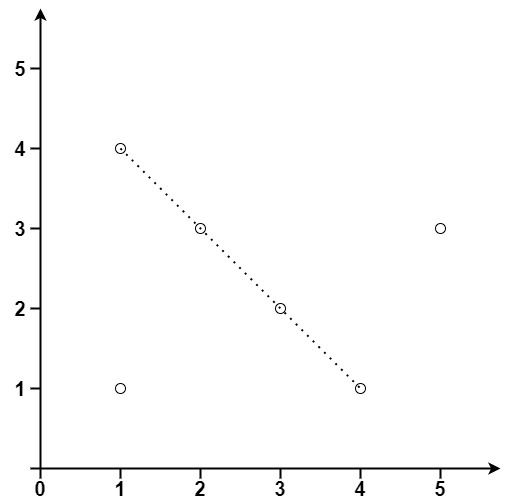
Solution:

假设直线一定经过\(points[i]\), 那么最多还能经过多少个点?

把\(points[i] = (x, y)\)当作坐标原点(所以直线一定经过坐标原点), 其余点\((x_2, y_2)\)的新坐标为\((x_2 - x, y_2 -y)\).

在直线一定经过坐标原点的情况下, 直线斜率为新坐标于原点连线的斜率. 斜率相同的点, 一定在同一条直线上.

斜率为 $$ k = \left { \begin{align} &\frac{y_2 -y}{x_2-x}, & x_2 \neq x \ &\infty, & x_2 = x \end{align}\right. $$ 用哈希表统计斜率的出现次数, 用出现次数的最大值加一(加上\(points[i]\)这个点), 更新答案的最大值.

细节

  1. 本题数据范围小，用浮点数表示斜率是正确的。
  2. 内层循环只需枚举下标在 \([i+1,n−1]\) 中的点。为什么？因为一条直线上的点一定有一个是下标最小的，外层循环枚举到这个点时，内层循环就能枚举到直线上的其余点了。

答疑

问：什么情况下用浮点数是错的？

答：取两个接近 1 但不相同的分数 \(\frac{a}{a + 1}\)和\(\frac{a - 1}{a}\), 根据 IEEE 754，在使用双精度浮点数的情况下，如果这两个数的绝对差\(\frac{1}{a(a+1)}\)比\(2^{-52}\) 还小，那么计算机可能会把这两个数舍入到同一个附近的浮点数上。所以当 a 达到 \(2^{26} \approx 6.7 \cdot 10^7\)的时候, 用浮点数就不一定对了. 本题数据范围只有\(2\cdot 10^4\)可以放心地使用浮点数除法.

class Solution {
    public int maxPoints(int[][] points) {
       int n = points.length;
       int ans = 0;
       for (int i = 0; i < n - 1; i++){
        int[] p = points[i];
        Map<Double, Integer> cnt = new HashMap<>();
        for (int j = i + 1; j < n; j++){
            int[] q = points[j];
            int dx = q[0] - p[0];
            int dy = q[1] - p[1];
            double k = dx != 0 ? (double) dy / dx : Double.POSITIVE_INFINITY;
            if (k == 0){ // 把 -0.0 转成 0.0
                k = 0;
            }
            int c = cnt.merge(k, 1, Integer::sum); // cnt[k]++;
            ans = Math.max(ans, c); // 这里没有算上p这个点, 最后再加一
        }
       }

       return ans + 1;
    }
}

// TC: O(n^2), 其中n是points的长度
// SC: O(n)

class Solution {
    public int maxPoints(int[][] points) {
        int n = points.length;
        if (n == 1){
            return 1;  // 只有一个点，最多共线点数就是 1
        }
        int result = 0;

        // 外层循环：依次选每个点作为“基准点”
        for (int i = 0; i < n - 1; i++){
            int x1 = points[i][0];
            int y1 = points[i][1];

                        // slopeMap：存每种斜率对应的共线点数
            Map<Double, Integer> cnt = new HashMap<>();

            // 内层循环：和基准点 i 比较其余点
            for (int j = i + 1; j < n; j++){
                int x2 = points[j][0];
                int y2 = points[j][1];

                double slope;
                                // 处理垂直线（x 相同）避免除以 0
                if (x2 == x1){
                    slope = Double.POSITIVE_INFINITY;
                }else{
                    slope = (y2 - y1) * 1.0 /(x2 - x1);
                }
                                // 把 -0.0 统一成 0.0，避免浮点数问题
                if (slope == 0){
                    slope = 0.0;
                }
                                // 从哈希表取当前斜率的出现次数（默认 1 表示当前两点）
                int count = cnt.getOrDefault(slope, 1) + 1;
                                // 更新哈希表
                cnt.put(slope, count);
                                // 更新当前最大共线点数
                result = Math.max(result, count);
            }
        }
        return result;
    }
}

// TC: O(n^2)
// SC: O(n)

class Solution {
    public int maxPoints(int[][] points) {
        int n = points.length;
        if (n == 1){
            return 1;
        }

        int result = 0;
        for (int i = 0; i < n; i++){
            Map<Double, Integer> map = new HashMap<Double, Integer>();
          // slope, count 
            int x1 = points[i][0];
            int y1 = points[i][1];
            for (int j = 0; j < n; j++){
                if (i == j){
                    continue;
                }
                int x2 = points[j][0];
                int y2 = points[j][1];


                //if denominator is not zero. calculate slope
                double slope = (y2 - y1) * 1.0d / (x2 - x1) * 1.0d;

                int count = map.getOrDefault(slope, 1) + 1; 
                // how much points on this line

                // update max variable
                result = Math.max(result, count);

                map.put(slope, count);
            }

        }

        return result;
    }
}

// TC: O(n^2)
// SC: O(n)

在 Java 的浮点数运算（double 或 float）中：

“除以 0” 不会抛异常，而是得到特殊值：

运算 结果
1.0 / 0.0 Infinity
-1.0 / 0.0 -Infinity
0.0 / 0.0 NaN

这不是好习惯.