Skip to content

134. Gas Station

There are n gas stations along a circular route, where the amount of gas at the ith station is gas[i].

You have a car with an unlimited gas tank and it costs cost[i] of gas to travel from the ith station to its next (i + 1)th station. You begin the journey with an empty tank at one of the gas stations.

Given two integer arrays gas and cost, return the starting gas station's index if you can travel around the circuit once in the clockwise direction, otherwise return -1. If there exists a solution, it is guaranteed to be unique

Example 1:

Input: gas = [1,2,3,4,5], cost = [3,4,5,1,2]
Output: 3
Explanation:
Start at station 3 (index 3) and fill up with 4 unit of gas. Your tank = 0 + 4 = 4
Travel to station 4. Your tank = 4 - 1 + 5 = 8
Travel to station 0. Your tank = 8 - 2 + 1 = 7
Travel to station 1. Your tank = 7 - 3 + 2 = 6
Travel to station 2. Your tank = 6 - 4 + 3 = 5
Travel to station 3. The cost is 5. Your gas is just enough to travel back to station 3.
Therefore, return 3 as the starting index.

Example 2:

Input: gas = [2,3,4], cost = [3,4,3]
Output: -1
Explanation:
You can't start at station 0 or 1, as there is not enough gas to travel to the next station.
Let's start at station 2 and fill up with 4 unit of gas. Your tank = 0 + 4 = 4
Travel to station 0. Your tank = 4 - 3 + 2 = 3
Travel to station 1. Your tank = 3 - 3 + 3 = 3
You cannot travel back to station 2, as it requires 4 unit of gas but you only have 3.
Therefore, you can't travel around the circuit once no matter where you start.

Constraints:

  • n == gas.length == cost.length
  • 1 <= n <= 105
  • 0 <= gas[i], cost[i] <= 104

Solution:

核心思路：“已经在谷底了，怎么走都是向上。”

来看看示例 1 是怎么算的（点击下面播放按钮）：

img

img

img

img

img

img

img

img

注：把数组复制一份，意思是 gas=gas+gas=[1,2,3,4,5,1,2,3,4,5]。

对于示例 2，由于 gas 元素和小于 cost 元素和，油量不够我们跑一圈，答案一定是 −1。

如果 gas 元素和大于等于 cost 元素和，答案是否一定存在？如何找到答案？

从示例 1 的计算过程可以发现，我们可以先计算从 0 号加油站出发的油量变化，然后从中找到油量最低时所处的加油站（3 号加油站），即为答案。

有没有可能从 3 号加油站出发，某个时刻油量变成负数呢？

这是不会的，请看下图：

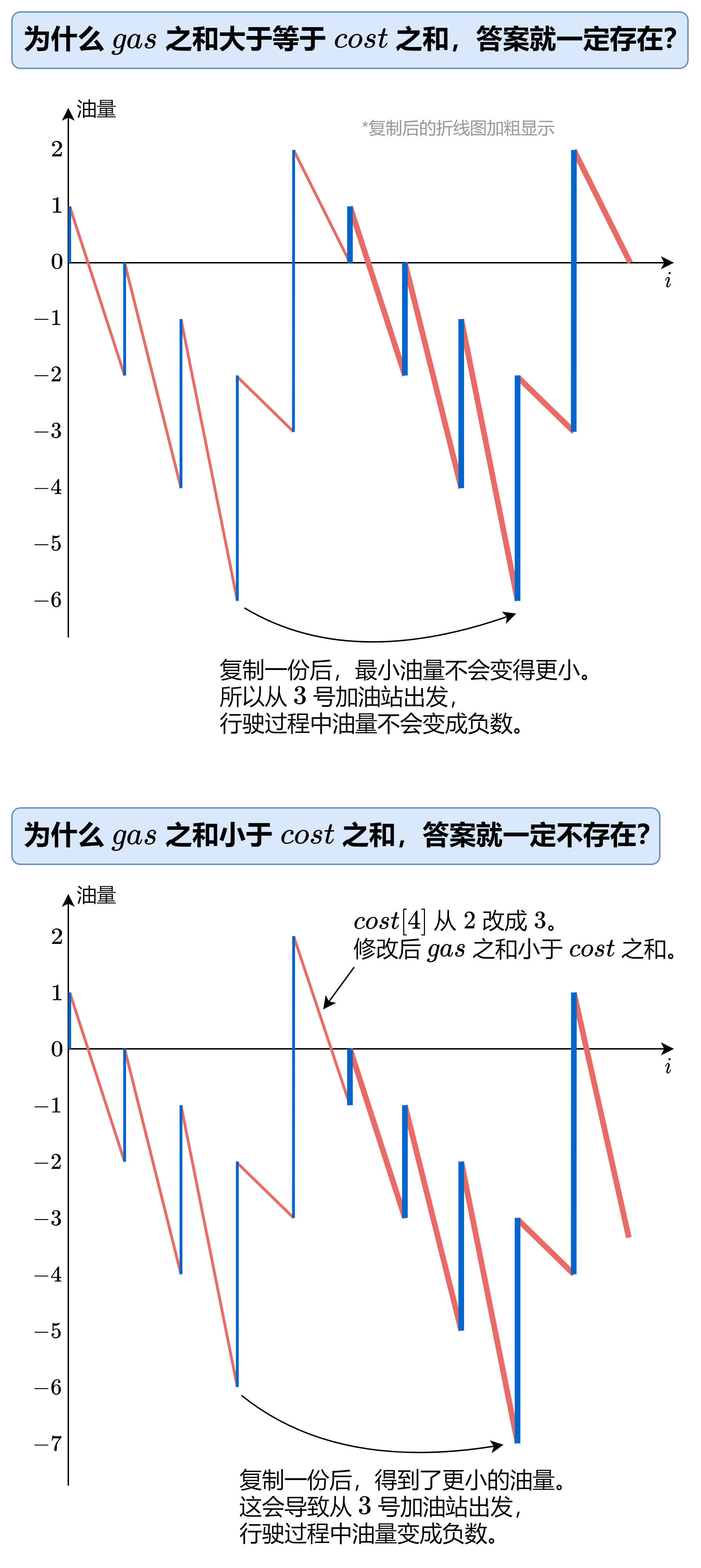
lc134-prove-c.png

⚠注意：gas 之和减去 cost 之和，对应图中复制的折线图的初始油量。如果不是负数，那么复制后的折线图的最小值，不会比第一段的最小值还小。如果是负数，那么复制后的折线图的最小值，比第一段的最小值还小，这会导致从第一段的最小值出发，行驶过程中油量会变成负数。

答疑 问：下面的代码，是否有可能算出 ans=n？

答：不会，如果最后一轮循环 s<minS，那么 s 必然小于 0，这会导致最终返回 −1。

class Solution {
    public int canCompleteCircuit(int[] gas, int[] cost) {
        int result = 0;
        int total = 0;
        int cur = 0;

        for (int i = 0; i < gas.length; i++){
            total = total + gas[i] - cost[i];

            cur = cur + gas[i] - cost[i];

            if (cur < 0){
                result = i + 1;
                cur = 0;
            }
        }

        if (total < 0){
            return -1; 
        }else{
            return result;
        }
    }
}


// TC: O(n)
// SC: O(1)

class Solution {
    public int canCompleteCircuit(int[] gas, int[] cost) {
        int result = 0;
        int minS = 0;
        int s = 0;
        for (int i = 0; i < gas.length; i++){
            s = s + gas[i] - cost[i]; // 在i处加油, 然后从i到i+1
            if (s < minS){
                minS = s; // 更新最小油量
                result = i + 1; // 注意s减去cost[i]之后, 汽车在i+1而不是i
            }
        }


        // 循环结束后, s即为gas之和减去cost之和
        if (s < 0){
            return -1;
        }else{
            return result;
        }
    }
}
// TC: O(n)
// SC: O(1)